Abstract

Refraction is a common phenomenon that happens every day. It is a natural concept that literally occurs every time light travels from one point to another. It is present in activities such as watching television, seeing your reflection in a mirror, and so on. In 1621, Dutch astronomer Willebrord Snell came up with the mathematic applications behind refraction hence Snell’s law. This law is the foundation of everything that involves Optics today. During the course of this experiment, we will aim to prove that Snell’s law works and is applicable in real life.

 

Introduction

The ultimate goal of this lab is to study the concept of refraction. Refraction is the change in direction, speed, and color of light when it passes from one medium to another. This lab in particular will focus on the change in direction of light through two different mediums by using the principles of Snell’s Law. Snell’s law states that the ratio of the angle of incidence to the angle of refraction of a wave as it travels through a boundary between two media is a constant designated as the index of refraction. The law is expressed as

n₁ and n₂  being the index of refraction of the two mediums.

When the angle of incidence reaches a certain value, the refracted ray of light has an angle of refraction of 90 degrees from the normal, this value is called the critical angle and is the largest value of angle of incidence at which refraction can still occur. The critical is calculated as

In the course of this experiment, if performed right the angles of refraction should be lower than the angles of incidence and there will be total refraction once the laser passes the critical angle.

 

Procedure

The materials needed to perform the lab were a semi-circular disc filled with water, a protractor, a laser, and tape. A thorough acquaintance was done with the laser and a piece of tape was wrapped around the keep the light on when needed. For more conclusive results the experiment was done in a dark room. The experiment consisted of two parts.

In the first part, the protractor was placed against the flat end of the semi-circular disc that was prefilled with water and the whole set was place on a white surface to allow a better vision. The laser was then turned on and a beam of light was sent through the semi-circular disc and the protractor, however, the light had to go through the reference mark (zero marks) of both instruments and this will help maintain the accuracy of the collected data. The incidence angles of the laser into the semi-circular disc were 0, 10, 20, 30, and 40 degrees, and the refraction angles were all recorded.

In the second part of the experiment, the protractor was removed, and a second white surface was placed on the right side of the semi-circular disc. The laser was turned on and rotated from 90 degrees to the left till a light beam appeared and then disappeared from the adjacent white surface we just added, and the critical angle was recorded.

 

Results

In the table below were recorded the angles of incidence and angle of refraction retrieved in the first part of the experiment.

Angle of incidence ()	Angle of refraction )
0	0
0.17	0.14
0.35	0.26
0.52	0.37
0.70	0.51

 

Table of incidence and refraction angles

In the second part of the experiment, our goal was to measure the critical angle; the critical angle is the angular value at which there is no longer a reflection of the emitted beam of light. The recorded critical angle in this experiment was of 43 degrees.

The following figure displays a plotted graph of the sin of the angle of incidence vs the sin of the angle of refraction.

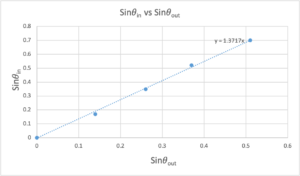
Fig 1: Graph of Sin𝜃_in vs Sin𝜃_out used to find the index of refraction the water

 

Calculations

From the graph, we retrieved an equation and that equation represents the index of the refraction of water since the water was the medium inside the semi-circular disc.

 

 

Discussion

Both data from the angles of refraction and incidence were used to plot a graph to retrieve the value of the index of refraction of water that was 1.37, therefore, having a percentage error of 3.01% which is reasonably low considering the possible error such reading and human error. The critical angle had a percentage error of 8.31%. Note that graphically determining the critical is quite tedious because not only the light beam is huge and retrieving the last angle value before it disappears can be quite challenging. Reading measures from the protractor in a dark room is very difficult so I would recommend using a flashlight for that specific part.

 

Conclusion

Snell’s law was at the center of our experiment today, we respectively found the index of refraction of water and the critical angle pass which there will be total refraction. Both objectives and hypothesis were met during this lab since we understood Snell’s law and how it leads to a critical angle and as predicted the refraction angle was lower than the incidence angles. One could also wonder what the importance of Snell’s law in real life. And an obvious answer would be prescribed glasses because the same mathematics is used to make glasses to adjust the eyes’ anomalies.

 

References

Katz, Deb. “Snell’s Law.” Physics for Engineers and Scientists, 1st ed., Cengage, 2016, pp. 371–402.

Hemmick, Tom. Refraction, 2017, www.youtube.com/watch?v=3nNsSi1eMGg.